关键词： 全国招教

《正方形性质的应用》

内容：

例5 求证：正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形。

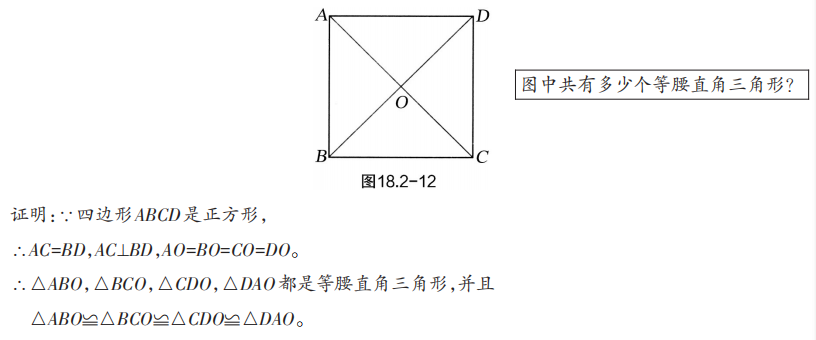
已知：如图18.2-12，四边形ABCD是正方形，对角线AC，BD相交于点O。

求证：△ABO，△BCO，△CDO，△DAO是全等的等腰直角三角形。

基本要求：

（1）书写完整的证明过程；

（2）试讲10分钟；

（3）要有合适的板书。

答辩题目：

1.说一说本节课的教学目标。

2.正方形有哪些性质？

试讲答案：

各位考官：大家好，我是初中数学组的XX号考生，今天我试讲的题目是《正方形性质的应用》，下面开始我的试讲。

一、复习旧知，导入新课

师：大家还记得上节课学习的正方形的性质吗？回忆一下。

师：学生1，你来说一下正方形有哪些性质，从正方形的边、角、对角线三方面来说。

师：同学们，他说的对吗？对。正方形的四条边相等，四个角都是直角，对角线互相垂直平分且相等。

师：同学们，根据前面学习平行四边形、矩形、菱形的性质的过程，我们在学完正方形的性质后该做什么了？

师：同学们很善于总结嘛，在学了性质后就要学习性质的应用。今天这节课就学习正方形性质的应用，即利用正方形的性质进行解题。

>>全国教师招聘官方客服微信<<

注意：备注网站才能通过哟！！！

公告解读 _历年考情_备考指导_海量资料_精品课程

如有任何报考疑问，添加客服老师微信咨询

二、探索新知

师：看黑板上这道题，我们一起分析一下。它的已知条件是什么？要证明的是什么？要想得出所给命题我们需要知道哪些信息？

师：学生2，你来说一说这道题给出的已知条件是什么。

师：学生2说给的条件就是四边形ABCD是正方形。那么能挖掘出来其他隐含条件吗？是不是正方形所具有的性质我们都能直接用来解题？算不算已知条件？

师：同学们回答得都不错，从图中我们可以得到AO=BO=CO=DO，AC=BD，且AC⊥BD。这些都可以看作已知条件。

师：接下来我们就一起探索证明过程。学生3，你说一下，我们要想证明结论的话首先需要证明哪些内容？

师：对，我们需要通过证明△ABO，△BCO，△CDO，△DAO是等腰直角三角形，然后再证明这些三角形都全等，达到证明要证命题的目的。

师：下面大家小组合作讨论具体步骤该怎样写。

师：第一组派代表来黑板上讲演一下你们组的讨论成果，注意证明题的书写格式。

师：第一组的证明过程是这样的：∵四边形ABCD是正方形，∴AC=BD，AC⊥BD，AO=BO=CO=DO，∴△ABO，△BCO，△CDO，△DAO都是等腰直角三角形，并且△ABO≌△BCO≌△CDO≌△DAO。

师：好，很规范。在证明命题时，可以用我们这节课所采用的步骤，先找已知，明确要证的是什么，再找能使这个结论成立的条件，从而推导证明结论。

三、课堂练习

师：我们看这道题目，如图，正方形ABCD中，AC，BD相交于O，MN∥AB，且MN分别交OA，OB于M，N，求证：BM=CN。

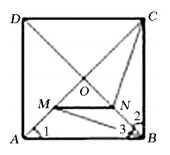
师：要想证明BM=CN，可以考虑先证什么？

师：学生4说得对，可以将线段放到三角形中，证三角形全等。

师：那大家小组讨论讨论可以证哪两个三角形全等。

师：第二组你们讨论的如何？

师：第二组代表说结合正方形的性质可以证明出△ABM≌△BCN，从而证明BM=CN。

师：其他组呢？有不一样的吗？

师：第三组代表说他们是先证明△CBM≌△DCN，从而证明BM=CN的。不错，虽然证明过程中利用的间接条件不一样，但都需要利用正方形的性质进行推导。

四、小结作业

师：这节课我们主要学习了什么？

师：对，这节课我们主要学习了应用正方形的性质解题的主要步骤，还学会了证明命题的一种思想方法。

师：课下大家总结一下平行四边形、矩形、菱形、正方形之间有什么样的关系。

五、板书设计

正方形性质的应用

边

角

对角线

我的试讲到此结束，谢谢各位考官的聆听。

答辩答案：

1.教学目标：

知识与技能：能说出正方形的定义和性质，会运用正方形的概念和性质进行有关的论证和计算。

过程与方法：经历观察、归纳获得数学猜想，发展合情推理能力，提高逻辑思维能力。

情感态度与价值观：激发学习热情，加深对“特殊与一般”的认识。

2.边：正方形的四条边都相等；对边平行。

角：正方形的四个角都是直角。

对角线：正方形的两条对角线相等，并且互相垂直平分，每一条对角线平分每一组对角。

2024年教师招聘官方微信客服

• 公告资讯
• 学习答疑
• 1对1指导
• 笔试资料
• 面试技巧
• 公开讲座

手机微信扫描左侧二维码，添加客服老师微信领取