关键词: 教师资格证

扫码添加专属备考顾问
▪ 0元领取考点真题礼包
▪ 获取1对1备考指导
《并集》
内容:
在上述两个问题中,集合A、B与集合C之间都具有这样一种关系:集合C是由所有属于集合A或属于集合B的元素组成的。
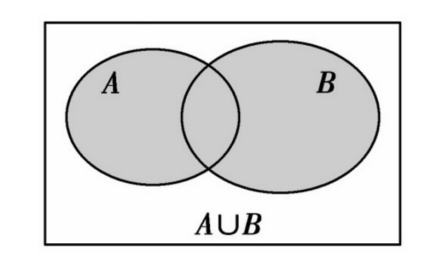
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(unio set),记作A∪B(读作“A并B”),即A∪B={xlx∈A或x∈B},可用Venn图1.1-2表示。

这样,在问题(1)(2)中,集合A与B的并集是C,即A∪B=C。
例4 设A={4,5,6,8},B={3,5,7,8},求A∪B。
基本要求:
(1)试讲时间10分钟左右;
(2)讲解要目的明确、条理清楚、重点突出;
(3)根据讲解的需要适当板书;
(4)讲解清楚并集的概念,学生会求两个集合的并集。
答辩题目:
1.集合的基本运算有哪些?
2.本节课的教学重难点是什么?
试讲答案:
各位考官:大家好,我是高中数学组的XX号考生,今天我试讲的题目是《并集》,下面开始我的试讲。
一、导入新课
师:同学们,前面的学习中,我们类比实数间的大小关系得到了集合之间的关系,那么,实数有加法运算,集合是否也可以“相加”呢?今天我们来一起探讨一下。
二、讲解新知
师:大家先来观察一下这些集合,说说集合C与集合A,B之间的关系。
师:当集合A={1,3,5},B={2,4,6},C={1,2,3,4,5,6,}时,请同学1来说说此时集合C与集合A,B之间的关系。
师:回答正确。此时集合C中的元素是集合A与集合B中元素的总和。
师:集合A={x|x是有理数},B={x|x是无理数},C={x|x是实数},这时三个集合之间的关系呢?
师:同学2反应很快,说集合C是由所有属于集合A或集合B的元素组成的。
师:这就是本节课我们要讲的集合的“并集”。一般地,由所有属于集合A或集合B的元素组成的集合,称为集合A与B的并集,记为A∪B,读作“A并B”,集合A与集合B的并集是C,即A∪B=C。
师:请同学们再举出一些其他集合的例子,并说出它们的并集。
师:我们大家都知道集合的表示方法有三种,下面我们看看如何用Venn图表示并集。
师:请大家根据前面我们做的第一道题作出对应的Venn图。想一想集合A与其自身作并集得到什么?集合A与空集作并集得到什么?并用符号语言表示出来。
师:大家的思路很清晰。集合A与自身作并集还是它本身,即A∪A=A,集合A与空集作并集仍是集合A,即A∪Ø=A。
三、课堂练习
师:我们一起来看这道题。集合A中有4,5,6,8四个元素,集合B中有3,5,7,8四个元素,求A与B的并集。
师:大家在求集合并集的时候注意集合元素的互异性。得出集合A与B的并集中有3,4,5,6,7,8这6个元素。
四、小结作业
师:通过这节课的学习,大家有什么收获?还有什么疑问吗?请大家完成课后习题。
五、板书设计
并 集
并集:A∪B={x|x∈A或x∈B}。
练习:A={4,5,6,8},B={3,5,7,8},求A∪B。
我的试讲到此结束,谢谢各位考官的聆听。
答辩答案:
1.集合的基本运算有并集、交集和补集。
(1)并集:一般地,由所有属于集合A或集合B的元素组成的集合,称为集合A与B的并集,记为A∪B(读作“A并B”),即A∪B={x|x∈A或x∈B}。
(2)交集:一般地,由属于集合A且属于集合B的所有元素组成的集合,称为集合A与B的交集,记作A∩B(读作“A交B”),即A∩B={x|x∈A且x∈B}。
(3)补集:一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U。对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作∁UA,即∁UA={x|x∈U且x∉A}。
2.结合本节课的教学内容以及学生已有的认知经验,我设置本节课的教学重点是:并集概念的理解。教学重点:求两个集合的并集。
在教学过程中,为了让学生充分理解什么是集合的并集,我会先给出两个简单的例子,并请学生观察每个例子中的三个集合之间有什么关系。学生很容易发现集合C是由所有属于集合A与集合B的元素组成的。这时我会顺势给出并集的概念,学生是不难理解并掌握的,同时为了加深学生对并集概念的理解,我会请学生再举出几个集合的例子,并说出它们的并集。
在理解概念的基础上,我会请学生求两个集合的并集。由于两个集合的并集仍是一个集合,而集合具有互异性,这是很多学生容易忽略的地方。通过题目的练习,不仅能使学生会求两个集合的并集,同时也加强对集合自身特性的掌握。

相关推荐:
手机登录确认
微信扫码下载
微信扫一扫,即可下载